Creating the Inputs to Design Rectifier Transformers
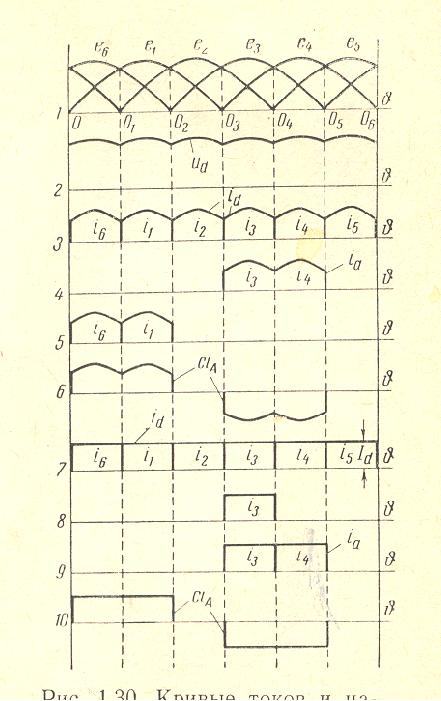
The input and no-load output voltages of a rectifier transformer normally have sine wave form. Due to the fact that a rectifier is a non-linear load, the transformer currents have harmonics. The type and the amount of harmonics depend on the rectifier circuit, the smoothing choke Xd and the transformer leaking reactance Xt.
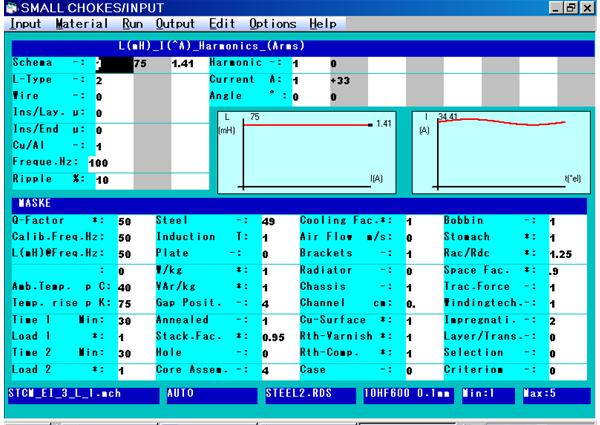
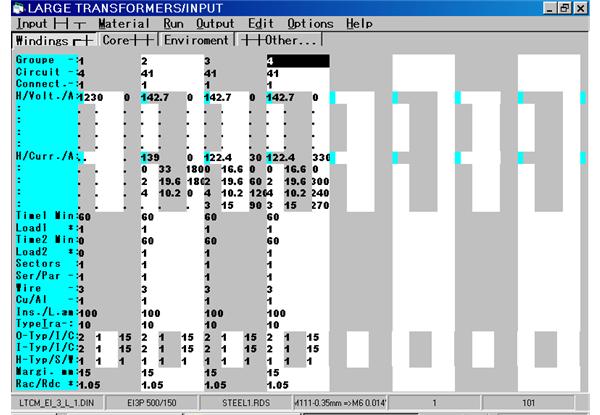
In the following text there are the most commonly rectifier circuits with the voltage and current diagrams with 5 harmonics of the transformer secondary currents which can be used in the Large Transformers Program. Also, there are screen captures of the input mask for Ud=100Vdc, Udiode=0 and Id=100Adc at Xt=0 and >> Xt.
Note that the program calculates the transformer AC output voltage on load. Due to this fact the no-load rectifier will be higher than 100Vdc but the on-load rectifier voltage will be lower than 100Vdc because the program does not calculate the commutation voltage drop of the rectifier. Using the calculated inductive short-circuit voltage you can easy recalculate the turns of the secondary winding.
List of the rectifier transformers shown below:
🔗 Single Phase, 2 Pulses Center Tap Rectifier with EI and UI core
🔗 Single Phase, 2 Pulses Bridge Rectifier
🔗 Three Phase DY Transformer with 3 Pulses Rectifier
🔗 Three Phase Transformer with 6 Pulses Bridge Rectifier
🔗 Three Phase DYY Transformer with 6 Pulses
🔗 Three Phase YYY Transformer with 6 Pulses 2×3 Diodes Rectifier, in Series connected
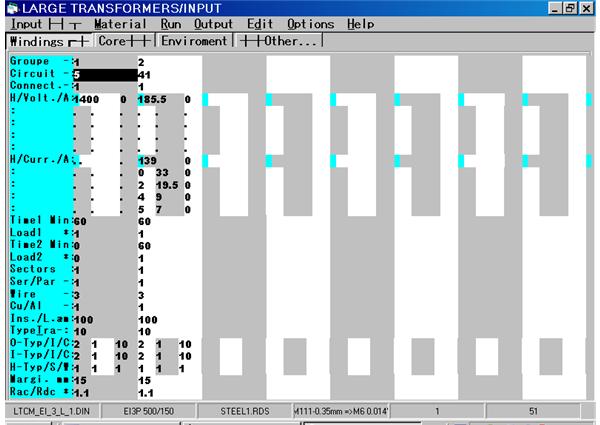
Single Phase, 2 Pulses Center Tap Rectifier with EI and UI core
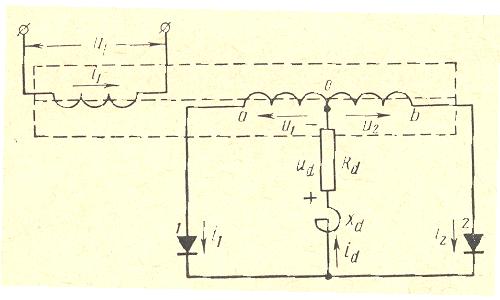

|
SECONDARY CURRENTS AND VOLTAGES at Xd=0 and Xt=0 |
||||
|
No-load voltage per winding |
U1=U2=1.11*(Ed+Udiode) |
|||
|
Harmonic k |
Isec.k.rms/Id |
Angle |
I22k.rms/Id |
Angle |
|
1 |
0.505 |
0 |
0.505 |
0 |
|
0=dc |
0.5 |
0 |
0.5 |
180 |
|
2 |
0.236 |
0 |
0.236 |
180 |
|
4 |
0.047 |
0 |
0.047 |
180 |
|
6 |
0.002 |
180 |
0.002 |
0 |
|
SECONDARY CURRENTS AND VOLTAGES at Xd=o/o and Xt=0 |
||||
|
No-load voltage per winding |
U1=U2=1.11*(Ed+Udiode) |
|||
|
Harmonic k |
I21k.rms/Id |
Angle |
I22k.rms/Id |
Angle |
|
1 |
0.45 |
0 |
0.45 |
0 |
|
0=dc |
0.5 |
0 |
0.5 |
180 |
|
3 |
0.15 |
180 |
0.15 |
180 |
|
5 |
0.09 |
0 |
0.09 |
0 |
|
7 |
0.065 |
180 |
0.065 |
180 |
In order to get symmetrical operation mode of both secondary windings both secondary windings have to have equal short-circuit voltages. This condition can be realized when the secondary windings are wound bifilar (not supported by program) or if the secondary windings are made in 2 sectors which are cross connected : the sector 1 of the secondary 1 in series with the sector 2 of the secondary 2, …) The following construction is not optimal but it is a good compromise.
Due to the fact that the input for design a transformer with an UI core is per leg all voltages in the input mask above have to be divided by 2.
For optimal, symmetrical operation mode for both secondary windings the inside secondary winding on the leg 1 has to be connected with outside secondary winding on the leg 2, … . Note that the parallel connection of the primary windings is allowed only with this order of the secondary windings.
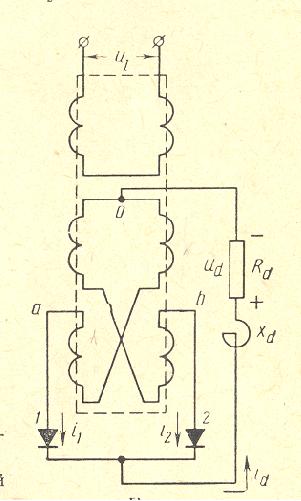
Single Phase, 2 Pulses Bridge Rectifier
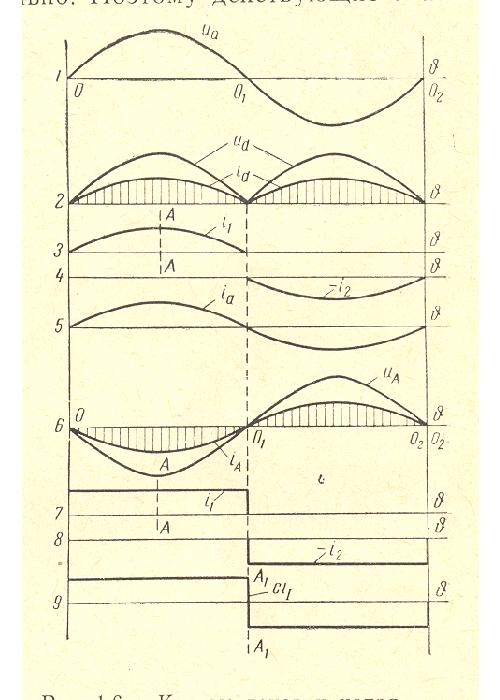
|
SECONDARY CURRENTS AND VOLTAGES at Xt=0 |
||||
|
No-load voltage per winding |
U2=1.11*(Ed+2*Udiode) |
|||
|
Smoothing choke |
Xd=0 |
Xd=o/o |
||
|
Harmonic k |
I21k.rms/Id |
Angle |
I22k.rms/Id |
Angle |
|
1 |
1.11 |
0 |
0.9 |
0 |
|
3 |
|
|
0.3 |
0 |
|
5 |
|
|
0.18 |
0 |
|
7 |
|
|
0.13 |
0 |
|
9 |
|
|
0.1 |
0 |
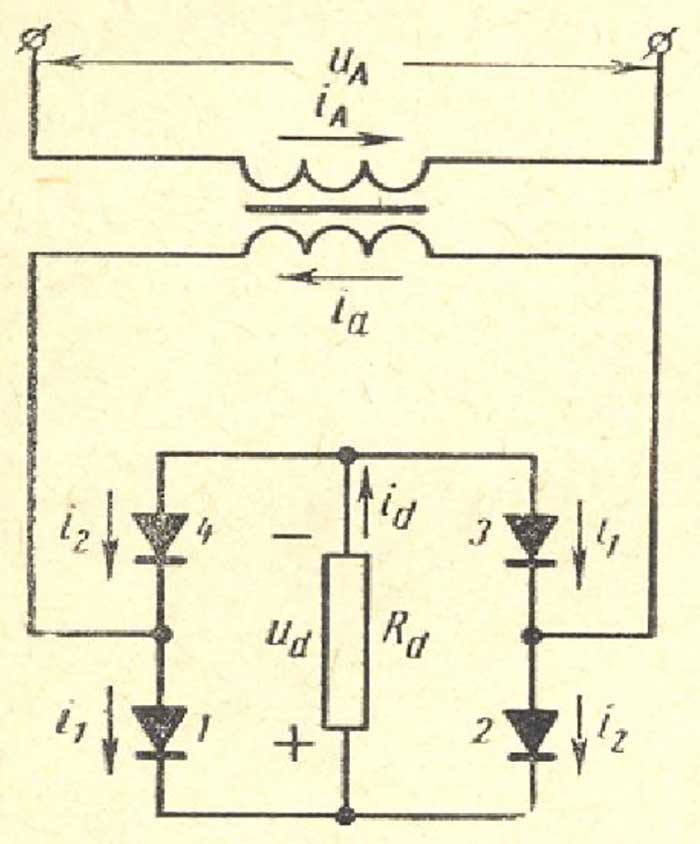
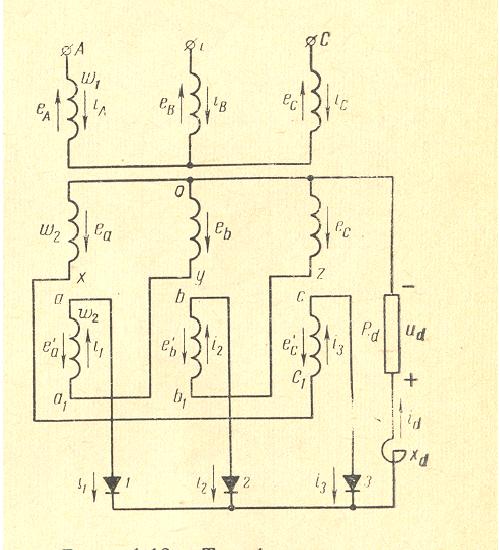
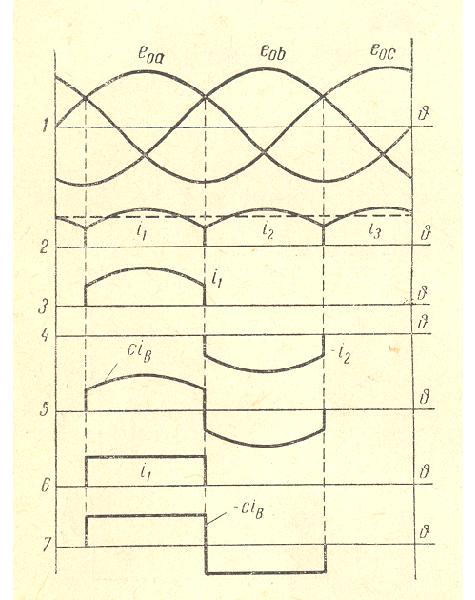
Three Phase DY Transformer with 3 Pulses Rectifier
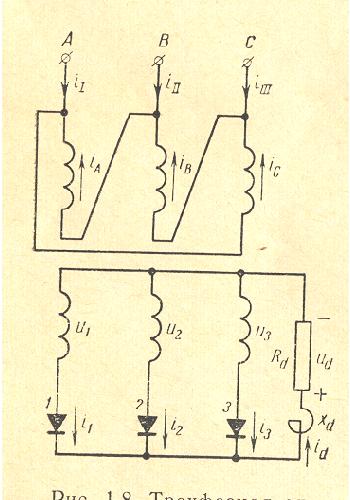
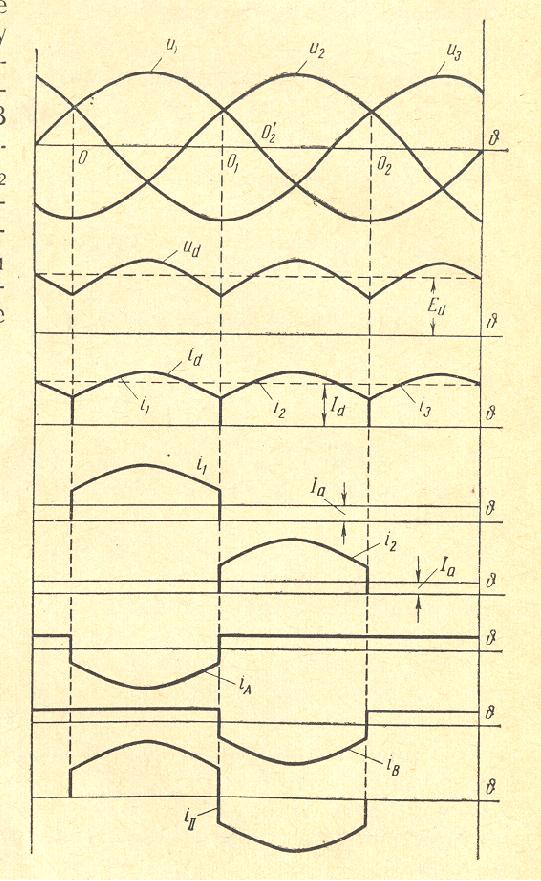
|
SECONDARY CURRENTS AND VOLTAGES at Xt=0 |
||||
|
No-load voltage per winding |
U1=U2=U3=0.855*(Ed+Udiode) |
|||
|
Smoothing choke |
Xd=0 |
Xd=o/o |
||
|
Harmonic k |
I21k.rms/Id |
Angle |
I22k.rms/Id |
Angle |
|
1 |
u.39 |
0 |
0.39 |
0 |
|
0=dc |
0.333 |
0 |
0.333 |
0 |
|
2 |
0.236 |
0 |
0.195 |
0 |
|
3 |
0.07 |
|
|
|
|
4 |
0.047 |
180 |
097 |
180 |
|
5 |
0.059 |
180 |
0.077 |
180 |
With the primary connection in delta the ampere-turns of the harmonics 2, 3, 4, … are balanced. These harmonics do not exist in the lines of the net.
Note that the ampere-turns of the secondary dc current are not balanced. For this reason there is a strong dc magnet field outside around the transformer.
Single Phase, 2 Pulses Bridge Rectifier Rectifier
|
SECONDARY CURRENTS AND VOLTAGES at Xd=o/o and Xt=0 |
||||
|
No-load voltage per winding |
Ea=Eb=Ec?=0.5*(Ed+Udiode/2) |
|||
|
Harmonic k |
I21k.rms/Id |
Angle |
I22k.rms/Id |
Angle |
|
1 |
0.39 |
0 |
0.39 |
0 |
|
0=dc |
0.333 |
0 |
0.333 |
180 |
|
2 |
0.19 |
0 |
0.19 |
0 |
|
4 |
0.09 |
0 |
0.09 |
0 |
|
5 |
0.07 |
180 |
0.07 |
0 |
|
SECONDARY CURRENTS AND VOLTAGES at Xd=0 and Xt=0 |
||||
|
No-load voltage per winding |
Ea=Eb=Ec==0.5*(Ed+Udiode/2) |
|||
|
Harmonic k |
I21k.rms/Id |
Angle |
I22k.rms/Id |
Angle |
|
1 |
0.39 |
0 |
0.39 |
0 |
|
0=dc |
0.333 |
0 |
0.333 |
180 |
|
2 |
0.236 |
0 |
0.236 |
0 |
|
3 |
0.07 |
0 |
0.07 |
180 |
|
4 |
0.047 |
180 |
0.047 |
0 |
Note that the input is per leg. All voltages are per leg The phase angle of the primary voltage on the leg is the reference angle. Normally it is set to “0”.
Phase difference between the currents of 2 secondary windings on the same leg is 60° (set with angles 30° and 330°, +- 30° to the peumary voltage)
The harmonics 0, 2, 3, 4, … are balanced within the secondary windings and do not exist in the primary.
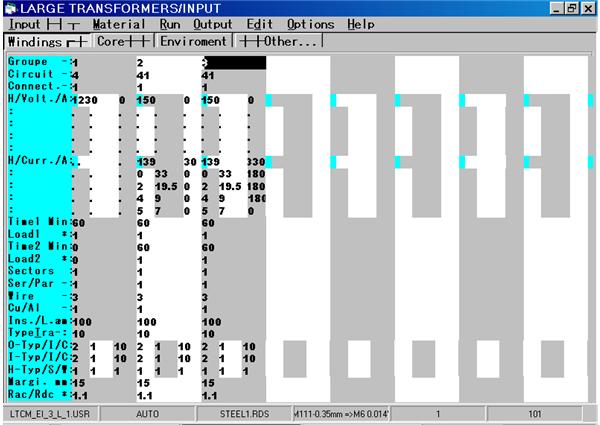
Three Phase Transformer with 6 Pulses Bridge
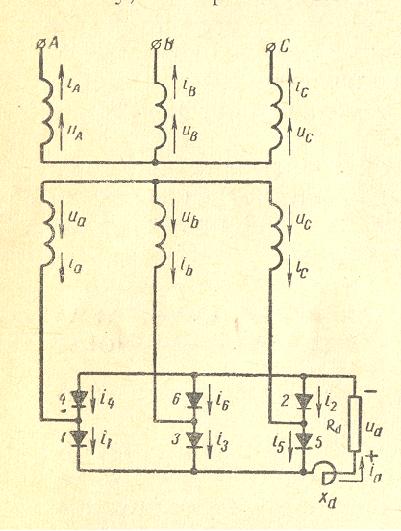
Rectifier
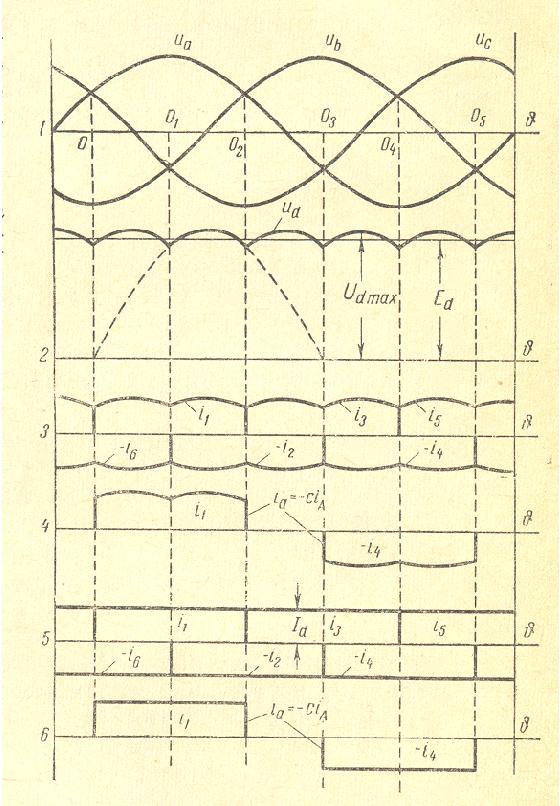
|
SECONDARY CURRENTS AND VOLTAGES at Xt=0 |
||||
|
No-load voltage per winding |
Ua=Ub=Uc=0.427*(Ed+2*Udiode) |
|||
|
Smoothing choke |
Xd=0 |
Xd=o/o |
||
|
Harmonic k |
I21k.rms/Id |
Angle |
I22k.rms/Id |
Angle |
|
1 |
0.808 |
0 |
0.779 |
0 |
|
5 |
0.177 |
|
0.155 |
180 |
|
7 |
0.088 |
180 |
0.111 |
0 |
|
11 |
0.071 |
0 |
0.07 |
180 |
|
13 |
0.05 |
180 |
0.06 |
0 |
Three Phase DYY Transformer with 6 Pulses
2×3 Diodes Rectifier
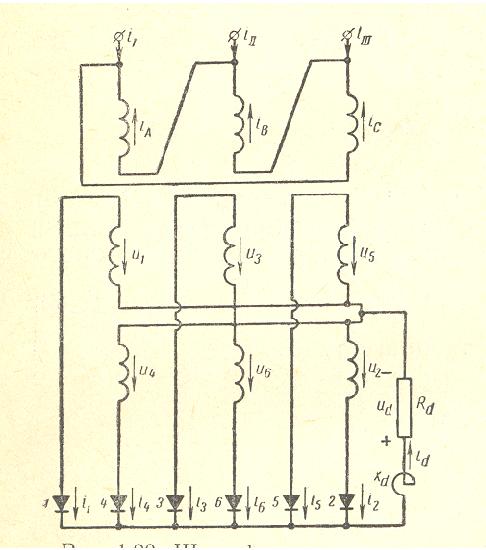
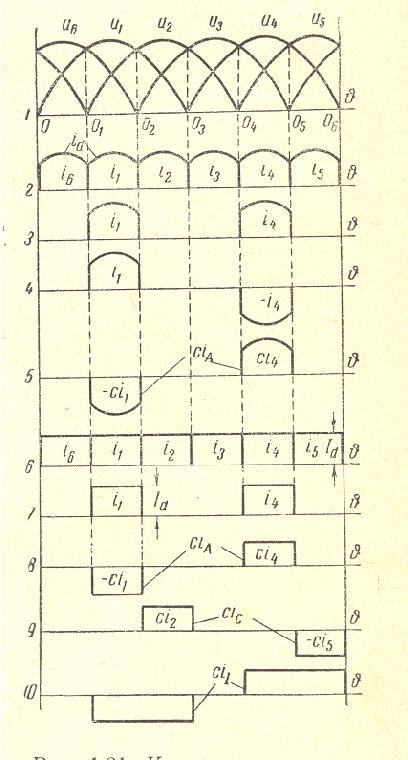
|
SECONDARY CURRENTS AND VOLTAGES at Xd=0 and Xt=0 (Line 2 and 4) |
||||
|
No-load voltage per winding |
U1=U4 = 0.74*(Ed+Udiode) |
|||
|
Harmonic k |
I21k.rms/Id |
Angle |
I22k.rms/Id |
Angle |
|
1 |
0.224 |
0 |
0.224 |
0 |
|
0=dc |
0.166 |
0 |
0.166 |
180 |
|
2 |
0.196 |
0 |
0.196 |
180 |
|
3 |
0.153 |
0 |
0.153 |
0 |
|
4 |
0.096 |
180 |
0.096 |
0 |
|
SECONDARY CURRENTS AND VOLTAGES at Xd=o/o and Xt=0 (Line 2 and 8) |
||||
|
No-load voltage per winding |
U1=U4 = 0.74*(Ed+Udiode) |
|||
|
Harmonic k |
I21k.rms/Id |
Angle |
I22k.rms/Id |
Angle |
|
1 |
0.224 |
0 |
0.224 |
0 |
|
0=dc |
0.166 |
0 |
0.166 |
180 |
|
2 |
0.19 |
0 |
0.19 |
180 |
|
3 |
0.15 |
0 |
0.15 |
0 |
|
4 |
0.097 |
180 |
0.097 |
0 |
There are 3 windings per leg: primary in delta connection and 2 secondary windings in star connection with phase difference of 180°.
The harmonics 0, 2, 4 ,8… are balanced within the secondary windings. 3. harmonic is balanced within the delta of the primary winding.
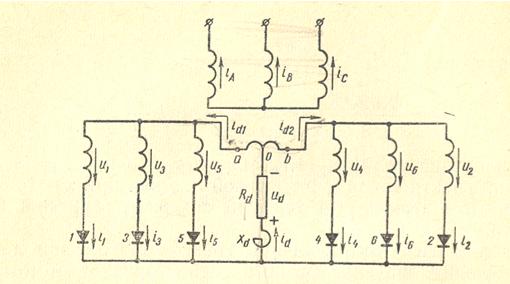
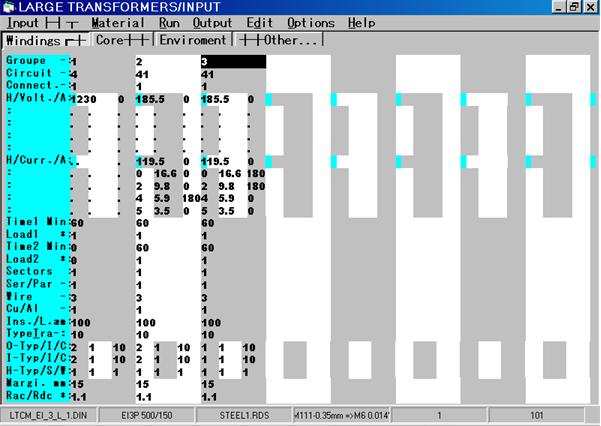
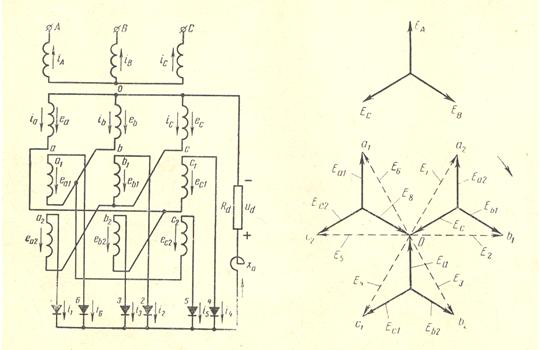
Three Phase YYY Transformer with 6 Pulses
2×3 Diodes Rectifier, in Series connected
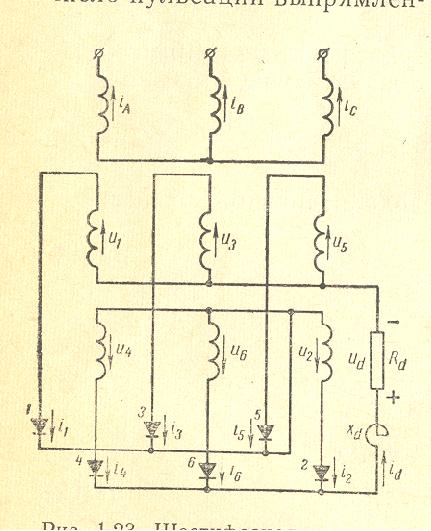
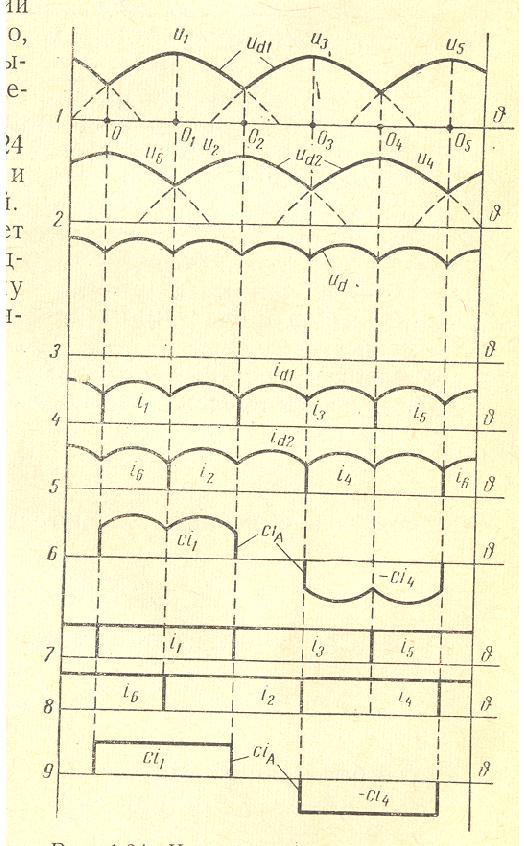
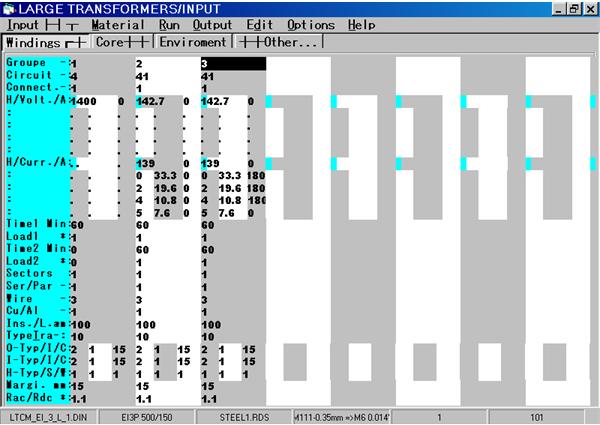
Three Phase YYY Transformer with 6 Pulses 2×3 Diodes Rectifier, parallel connected
via Drainage Reactor
|
SECONDARY CURRENTS AND VOLTAGES at Xd=0, Xr=o/o and Xt=0 (Line 1 and 3) |
||||
|
No-load voltage per winding |
U1=U4 =0.855*(Ed+Udiode) |
|||
|
Harmonic k |
I21k.rms/Id |
Angle |
I22k.rms/Id |
Angle |
|
1 |
0.195 |
0 |
0.195 |
0 |
|
0 |
0.166 |
0 |
0.166 |
180 |
|
2 |
0.098 |
0 |
0.098 |
180 |
|
4 |
0.051 |
0 |
0.051 |
180 |
|
5 |
0.044 |
0 |
0.044 |
0 |
|
SECONDARY CURRENTS AND VOLTAGES at Xd=o/o, Xr=o/o and Xt=0 (Line 1 and 5) |
||||
|
No-load voltage per winding |
U1=U4?=(Ed+Udiode)/1.17 |
|||
|
Harmonic k |
I21k.rms/Id |
Angle |
I22k.rms/Id |
Angle |
|
1 |
0.195 |
0 |
0.195 |
0 |
|
0 |
0.166 |
0 |
0.166 |
|
|
2 |
0.098 |
0 |
0.098 |
180 |
|
4 |
0.059 |
180 |
0.059 |
0 |
|
5 |
0.038 |
0 |
0.038 |
0 |
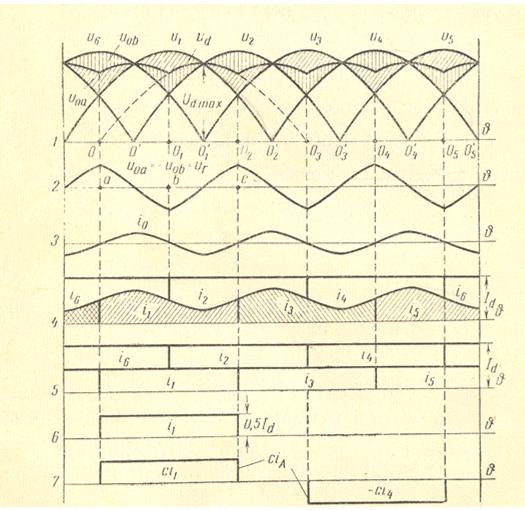
This circuit has two 3 pulse rectifiers, connected parallel via the drainage reactor. The ampere-turnsof the harmonics 0, 2, 4, 8, … are balanced within the secondary windings. Normally the inductance of the drainage reactor should be set so high that the 3. harmonic of the transformer current is not higher than 0.5-1% of the DC output current. If so, then the primary must not be connected in delta. For an optimal current distribution between the parallel connected rectifiers the secondary windings have to have equal short-circuit voltages. For this reason the order of the windings per leg should be: secondary 1- primary – secondary 2 (NOT USED IN THE FOLLOWING INPUT).
In order to create the input for the design of the drainage reactor we need to know the inductance Lab for:
- max. value of the 3. current harmonic I3ab = 0.01*Id = 1Arms
- f = 150Hz
- nominal rms value of the 3. voltage harmonic U3oa = Ed/4/1.41=17.7Vrms
- L0a=U3oa/I3ab/2/pi/f = 17.7/1/6.28/150 =18.7mH
- Lab=4*187 =75mH
- If the asymmetry of the rectifier currents is q% of the DC output current then 2.41 instead 1.41
Note that +50 means that this current does NOT produce any magnetizing of the core.
Three Phase Y/YZZ Transformer with 6 Pulses
3×2 Diodes Rectifier
|
SECONDARY CURRENTS AND VOLTAGES at Xd=0 and Xt=0 (Line 2, 3 and5) |
||||
|
No-load voltage per winding |
Ea=Ea1=Ea2=0.427*(Ed+Udiode/2) |
|||
|
Harmonic k |
I21k.rms/Id |
Angle |
I22k.rms/Id |
Angle |
|
1 |
0.224 |
30/330 |
0.39 |
0 |
|
0=dc |
0.166 |
0 |
0.333 |
180 |
|
2 |
0.196 |
60/300 |
0.196 |
180 |
|
3 |
0.15 |
|
0 |
180 |
|
4 |
0.102 |
120/240 |
0.102 |
0 |
|
SECONDARY CURRENTS AND VOLTAGES at Xd=o/o and Xt=0 (Line 2, 7 and 9) |
||||
|
No-load voltage per winding |
Ea=Ea1=Ea2=0.427*(Ed+Udiode/2) |
|||
|
Harmonic k |
I21k.rms/Id |
Angle |
I22k.rms/Id Ia |
Angle |
|
1 |
0.224 |
30/330 |
0.39 |
0 |
|
0=dc |
0.166 |
0/0 |
0.333 |
180 |
|
2 |
0.196 |
60/300 |
0.196 |
180 |
|
3 |
.15 |
90/270 |
0 |
0 |
|
4 |
0.1081 |
120/240 |
0.108 |
0 |
Note that there are 4 windings per leg; for example A, a, a1 and a2. 3rd harmonic is balanced within the windings a1 and a2. The harmonics 0,2,4,8,.. are balanced within the secondary windings a, a1 and a2.
Three Phase D/3x Center Tap Windings with 3×2 Diodes Rectifier, connected parallel via 3 Phase Drainage Reactor
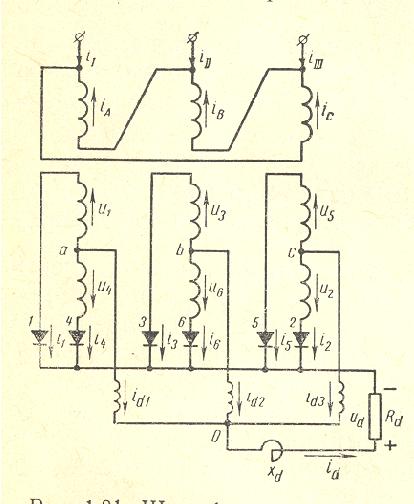
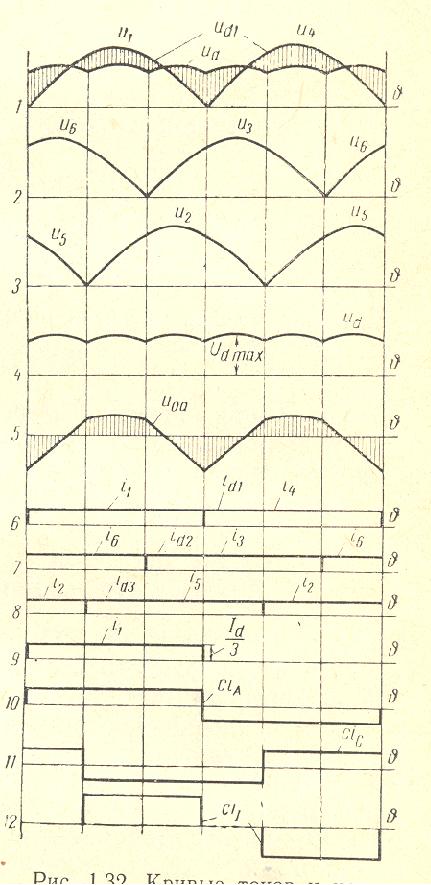
|
SECONDARY CURRENTS AND VOLTAGES at Xd=o/o, Xr=o/o and Xt=0 |